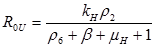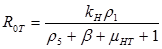3.2
Impact Factor
ISSN: 1837-9664
J Cancer 2012; 3:262-268. doi:10.7150/jca.4161 This volume Cite
Research Paper
A Mathematical Model of Human Papillomavirus (HPV) in the United States and its Impact on Cervical Cancer
Department of Mathematics and Computer Science, Alabama State University, 915 S. Jackson St., Montgomery, AL 36101, USA.
Received 2012-1-28; Accepted 2012-6-5; Published 2012-6-9
Abstract
Background: Mathematical models can be useful tools in exploring disease trends and health consequences of interventions in a population over time. Most cancers, in particular cervical cancer, have long incubation periods. The time from acquisition of HPV infection to development of invasive cancer can be up to two decades or more. Mathematical models can be used to translate short-term findings from prevention and mitigations trials into predictions of long-term health outcomes. The main objective of this paper is to develop a mathematical model of HPV for African American women (AAW) in the United States and give quantitative insight into current U.S. prevention and mitigations against cervical cancer.
Methods: A compartmental mathematical model of the cycle of HPV that includes the choices individuals make once they become infected; treatment versus no treatment, was developed. Using this mathematical model we evaluated the impact of human papillomavirus (HPV) on a given population and determined what could decrease the rate at which AAW become infected. All state equations in the model were approximated using the Runge-Kutta 4th order numerical approximation method using MatLab software.
Results: In this paper we found that the basic reproductive number ROU is directly proportional to the rate of infectivity of HPV and the contact rate in which a human infects another human with HPV. The ROU was indirectly proportional to the recovery rate plus the mortality by natural causes and the disease. The second ROT is also directly proportional to the rate of infectivity of HPV and contact rate in which humans infect another human with HPV and indirectly proportional to the recovery rate plus the mortality from HPV related cause and natural causes. Based on the data of AAW for the parameters; we found that ROU and ROT were 0.519798 and 0.070249 respectively. As both of these basic reproductive numbers are less than one, infection cannot therefore get started in a fully susceptible population, however, if mitigation is to be implemented effectively it should focus on the HPV untreated population as ROT is greater than 0.5.
Conclusion: Mathematical models, from individual and population perspectives, will help decision makers to evaluate different prevention and mitigation measures of HPV and deploy synergistically to improve cancer outcomes. Integrating the best-available epidemiologic data, computer-based mathematical models used in a decision-analytic framework can identify those factors most likely to influence outcomes and can help in formulating decisions that need to be made amidst considerable lack of data and uncertainty. Specifically, the model provides a tool that can accommodate new information, and can be modified as needed, to iteratively assess the expected benefits, costs, and cost-effectiveness of different policies in the United States. This model can help show the direct relationship between HPV and cervical cancer. If any of the rates change it will greatly impact the graphs. These graphs can be used to discover new methods of treatment that will decrease the rate of infectivity of HPV and Cervical cancer with time.
Keywords: Human Papillomavirus (HPV), reproductive number.
Introduction
Genital Human papillomavirus (HPV) is one of the most common sexually transmitted infections (STI) [1] and has been shown in epidemiological and molecular studies to be a necessary etiologic agent for cervical cancer [1-3]. The virus infects the skin and mucous membranes. There are more than 40 HPV types that can infect the genital areas of men and women, including the skin of the penis, vulva (area outside the vagina), and anus, and the linings of the vagina, cervix, and rectum. Most people who become infected with HPV do not even know that they have it. The HPV type 16 is the most common high-risk type, accounting for more than half (56%) of all cervical cancers [4]. Persistent infection with high-risk types of HPV is the most important risk factor for cervical cancer [5]. The long premalignant course of HPV infection means that screening programs can detect and treat early disease and prevent progression to cervical cancer.
In the United States, approximately 20 million Americans are currently infected with HPV, and another 6.2 million people become newly infected each year. At least 50% of sexually active men and women acquire genital HPV infection at some point in their lives [1]. Almost half of the infections are in people between 15 and 25 years of age [6].
Genital HPV is spread mainly by direct genital contact during vaginal, oral and/or anal sex. It is not spread through blood or body fluids. Infection is very common soon after a woman becomes sexually active. Oral-genital and hand-genital transmission of some genital HPV types is possible and has been reported. Transmission from mother to newborn during delivery is rare. When it occurs, it can cause warts in the infant's throat called respiratory papillomatosis [6].
Genital HPV usually has no symptoms, unless it is a type that causes genital warts. Genital warts may appear within weeks or months after contact with a partner who has HPV. Most people will never know they have HPV because they have no symptoms and the body's immune system causes the virus to become inactive. A small number of people with HPV will have the virus for longer periods of time [6].
About 99% of all cervical cancers are related to HPV. Of these, about 70% are caused by HPV types 16 or 18. About 500,000 pre-cancerous cell changes of the cervix, vagina, and vulva are diagnosed each year in the United States, and over half are related to HPV 16 and 18 [7]. Although all cervical cancers are related to HPV, most genital HPV infections do not cause cervical cancer. Research studies indicate that, most people who test positive for genital HPV DNA test negative later on, often within a 6 to 12 months period [1].
HPV cannot be treated, but most genital HPV infections resolve with the help of the body's immune system. About 70% of HPV infections appear to go away within a year and 90% within 2 years. Although HPV itself cannot be treated, the cellular changes that come from an HPV infection can be treated. For example, genital warts can be treated. Pre-cancerous cell changes caused by HPV can be detected by Pap tests and treated. Cervical, anal, and genital cancers can also be treated.
Getting the HPV vaccine before being exposed to HPV will prevent some HPV infections. Limiting the number of sex partners and avoiding sex with people who have had many other sexual partners decreases a person's risk of exposure to HPV. Human papilloma virus infections are very common, these afore mentioned precautionary measures are no guarantee that a person will not get HPV. Still, these measures may help reduce the number of times a person is exposed to HPV.
Condoms provide some, but not total, protection against HPV. The virus can spread during direct skin-to-skin contact before the condom is put on, and male condoms do not cover the entire genital area, especially in women. The female condom covers more of the vulva in women but has not been studied as carefully for its ability to prevent HPV. Condoms are very helpful, though, in protecting from other infections that can be spread through sexual activity.
In June of 2006, the Food and Drug Administration (FDA) approved a vaccine that prevents the 2 types of HPV (HPV 16 and 18) that cause 70% of all cervical cancers [7]. The vaccine also prevents 2 types of HPV (HPV 6 and 11) that cause 90% of all genital warts. This vaccine is named Gardasil®. In October 2009, Bivalent HPV (HPV2) which prevents the 2 types of HPV (HPV 16 and 18) for females 10 through 25 years of age was approved. Over the next few years, we can expect to see the licensing of one or more prophylactic vaccines against human papillomavirus (HPV) infection, considered a necessary precursor to cervical cancer.
HPV infection can be treated if detected in its earliest stages by annually having a papanicolaou test or pap smear, which is a scrapping of the cervix to detect abnormal cells [1]. Once dysplasia is noticed by genital warts, the individual should get a biopsy to better determine which region of the cervix is infected. Treatment options are freezing, laser surgery, or doing nothing. Sometimes the body will naturally heal itself but that is a high risk to take. Typically, HPV infection can be treated, but for individuals who do not regularly visit a gynecologist to check if they are infected, have a higher risk of HPV infection advancing to cervical cancer. Women fail to get regular checkups for various reason such as fear, the idea that “nothing is wrong”, “I cannot possibly get that”, and lack of monetary resources. The highest number of cervical cancer cases is found in resource poor populations of women in whom at least 80% of all incident cervical cancer and related mortality occurs [2]. They are not able to afford proper healthcare, but those who can should invest to prevent the HPV infection advancing to cervical cancer.
Although cervical cancer can be prevented, it is still the number two cancer killer of women [7]. The cancer begins in the cervix, the lower part of the uterus which extends to the vagina and is very important for child bearing and for controlling the blood flow during menstruation. Cervical cancer is caused by squamous or adenocarcinoma (non squamous) tumors and if treated in its early stages, the five year survival rate is very high [6]. There are four stages of cervical cancer: Stage 1 non invasive, Stage 2 cancer spreads outside cervix, Stage 3 advanced extends to pelvic wall, and Stage 4 most advanced and spreads to other organs [1]. Even though cervical cancer occurs in younger women it is mostly common in women between 35 and 55 years of age. These women tend to stop getting pap smears and do not realize they are at the most vulnerable ages. There are several available treatments for cervical cancer including hysterectomy, radiation, and chemotherapy. Although the cancer is a killer, women can overcome the cancer by taking better health precautions.
Methods
Mathematical models, from individual and population perspectives, will help decision makers to evaluate different prevention and mitigation scenarios against HPV infection. The models can deploy synergistically to analyze improvement of cancer outcomes, reduce disparities, and enhance the cost-effectiveness of cervical cancer prevention, treatment and control. Integrating the best-available epidemiologic data, computer-based mathematical models used in a decision-analytic framework can identify those factors most likely to influence outcomes. This can help decision makers in making decisions that need to be made amidst considerable lack of data and uncertainty due to the long incubation period of cancer.
Given the inevitable uncertainty around input parameters to many mathematical models, an important feature of many modeling efforts is the evaluation of these parameter values in reference to observed epidemiologic data. Our objectives in this paper are to: (1) describe a formal approach to the parameterization, calibration, and evaluation of an HPV infection model for the AAW in the United States; and (2) use this model to predict health outcomes, as well as the uncertainty surrounding these predictions, associated with vaccination against HPV infection, and combinations of vaccination and screening.
The Mathematical Modeling
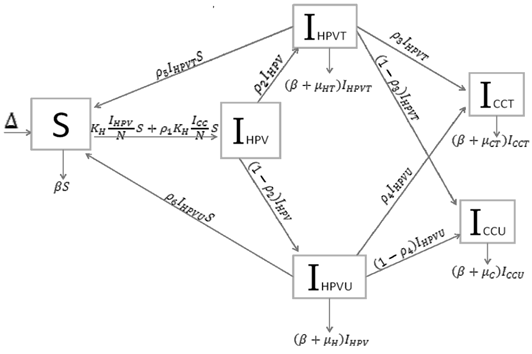
Based on the biology of HPV, and cervical cancer, we developed a system of sequence of differential equations that capture the dynamics of HPV and cervical cancer. The system was then analyzed using the method of the next generator operator, with a basic reproduction number. Parameters were defined and estimated (Table 1) and the model was developed considering all possible scenarios which individuals might take in regard to HPV and cervical cancer mitigations. This is shown as a flow diagram in which the boxes represent the different compartments and the arrows show the transitions between compartments (Figure 1).
Many diseases, especially diseases caused by viral agents, including HPV, smallpox, measles, and rubella (German measles), provide immunity against re-infection. Such diseases tend to occur in cycles of outbreaks due to the variation in number of susceptible individuals. In our model we used a compartmental model representing the progression of HPV disease from susceptible to HPV infection to cancer in five compartments. The susceptible population (S(t) over time) is African American Women older than 16. During an epidemic, the number of susceptible individuals falls rapidly as more of them are infected and thus progress to either the infected stage receiving treatment IHPVT(t) (the number of HPV the infected receiving treatment) or the infected stage receiving no treatment IHPVU(t) (the number of HPV infected receiving no treatment). Both the IHPVT(t) and IHPVU(t) can then progress to either the class of cervical cancer population of treated (ICCT (t)) or untreated (ICCU (t)). However, it is indicated in the literature that also both the IHPVT(t) and IHPVU(t) can revert to the susceptible stage (S(t)). The disease cannot break out again until the numbers of susceptible have built back up as a result of new born added into the susceptible compartment at a rate of Δ and also as a result of the reversion from IHPVT(t) and IHPVU(t). N is the total population (the sum of all the state populations), and that ICC is the sum of ICCT (t) and ICCU (t).
We derived the differential equations expressing the rate of change of the size of each of the five compartments of population. Using this model we evaluate the impact of HPV on AAW population in US and determine what can decrease the rate in which AAW become infected. The dynamics of the relationships between the AAW population and HPV disease and the behaviors were described by means of ordinary differential equations. All state equations in the model were approximated using the Runge-Kutta 4th order numerical approximation method using MatLab.
Parameter list and their estimates.
| Parameter estimate | Parameter description | Reference(s) |
|---|---|---|
| Δ = 16,821,072* | Human recruitment rate | [9] |
| KH = 0.80 | Rate at which humans infect other humans (effective contact rate) | [1] |
| β = 0.0576 | Per capita mortality rate of population | [9] |
| μHT = very close to 0 | Mortality rate of individuals infected with HPV receiving treatment | [1-7] |
| μH = very close to 0 | Mortality rate of individuals infected with HPV with no treatment | [1-7] |
| μCT = 0.05721 | Mortality rate of individuals with cervical cancer receiving treatment | [7] |
| μC = 0.00043 | Mortality rate of individuals with cervical cancer with no treatment | [7] |
| ρ1 = 0.31 | Rate of infectivity of HPV | [7] |
| ρ2 = 0.85 | Rate of infectivity of HPV receiving treatment | [7] |
| (1-r2) = 0.15 | Rate of infectivity of HPV receiving no treatment | [7] |
| ρ3 = 0.00035 | Rate of change of infection from HPV with treatment to cervical cancer | [1-2] |
| ρ4 = 0.1271 | Rate of change of infection from HPV with no treatment to cervical cancer | [1-2] |
| ρ5 = 0.30 | Recovery rate from HPV infection with treatment | [6-7] |
| ρ6 = 0.70 | Recovery rate from HPV infection without treatment | [6-7] |
*This is only the population of AAW 16 years and over in 2010. Men were not considered since they have no cervix.
Systems Dynamic Model of HPV in causation of CC.
The theory of biological evolution provides a dynamic method for predicting past and future population change. If we know a population's current composition and we can identify the fittest individuals, we can predict that population's future composition. However, when converting theory to prediction we stumble at one particular point: how does nature determine fitness? Fitness is a flexible concept that can be defined in different ways depending on the evolutionary problem being addressed. The evolutionary ecology concept of fitness is conventionally defined as the “reproductive success” of a phenotype or adaptation. In infectious disease research, the most commonly invoked measure of reproductive success is the basic reproductive number R0.
R0 is commonly used in mathematical epidemiology as summary statistics for the size and controllability of epidemics. To study evolution problems where the host population size is changing, measures like the ultimate proliferation rate must be used. For infectious diseases, this means the number of new infections caused by a typical case in a completely susceptible population. In several archetypal epidemiology models, strains of disease with higher R0 values out-compete strains with lower R0 values, leading to a rule-of-thumb that evolution maximizes R0.
The next generation operator approach: R0 is often found through the study and computation of the eigenvalues of the Jacobian at the disease- or infectious-free equilibrium. Diekmann [8] follow a different approach called the next generation operator approach. They define R0 as the spectral radius of the “next generation operator”. The details of this approach are outlined in the rest of this section. First, we consider the case where heterogeneity is discrete, that is, the case where heterogeneity is defined using groups defined by fixed characteristics, that is, for epidemiological models that can be written in the form:
where X ∈ IRr; Y ∈ IRs, Z ∈ IRn, r; s; n ≥ 0, and h(X; 0; 0) = 0. The components of X denote the number of susceptibles, recovered, and other classes of non-infected individuals. The components of Y represent the number of infected individuals who do not transmit the disease (various latent or non-infectious stages). The components of Z represent the number of infected individuals capable of transmitting the disease (e.g., infectious and non-quarentined individuals). Let U0 = (X*; 0; 0) ∈ IRr+s+n denote the disease-free equilibrium, that is,
f(X*,0,0)=g(X*,0,0)=h(X*,0,0)=0.
Assume that the equation g(X*; Y; Z) = 0 implicitly determines a function Y = ĝ(X*; Y ). Let A = DZh(X*; ĝ(X*; 0); 0) and further assume that A can be written in the form A = M - D, with M ≥ 0 (that is, mij ≥ 0) and D > 0, a diagonal matrix.
The spectral bound of matrix B is denoted by m(B) = sup {ℜλ : λ∈σ(B)}, where ℜλ means the real part of λ, while 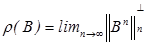 denotes the spectral radius of B. The proof of the following theorem involving matrix A is found in Diekmann [8]:
denotes the spectral radius of B. The proof of the following theorem involving matrix A is found in Diekmann [8]:
Either
m(A)<0 ⇔ ρ(MD-1)<1
or
m(A)>0 ⇔ ρ(MD-1)>1
The basic reproductive number is defined as the spectral radius (dominant eigenvalue) of the matrix MD-1, that is,
R0 =ρ(MD-1)
Using a system of five differential equations the spread of HPV infection is described, based on the five compartments. When developing the model, we did not consider those cases where a susceptible individual becomes infected with cervical cancer, since those cases are rare. As IHPV is a transition compartment and the time it takes to move to treated or untreated is shorter time scale as compared to the other five compartment and hence is not included in the system of differential equations. Listed below are the differential equations (DE) from the model. The positive terms are what are entering the compartment and the negative terms are what are leaving the compartment, respectively.
Two vectors, V and F were used to find R0.
Using Maple 6.0, we used the Next Generator Process to find the exact value of R0 using the two vectors above.
If R0U is less than 1 and R0T is less than 1, then the system of differential equations is stable. This means the DE is asymptotically stable. The values for the parameters were found from various sources in the literature.
Results and Conclusion
Analytical results of the model show that the quantity R0U is directly proportional to the rate of infectivity of HPVU and inversely proportional to the rates of HPVU recovery and the mortality rate of HPVU (natural and due to HPVU) population. Similarly, R0T is directly proportional to the rate of infectivity of HPVT and inversely proportional to the rates of HPVT recovery and the mortality rate of HPVT (natural and due to HPVT) population. The results of the numerical simulations, using data from different sources in the literature [1-7], and other resources like CDC, confirmed and extended the analytic results.
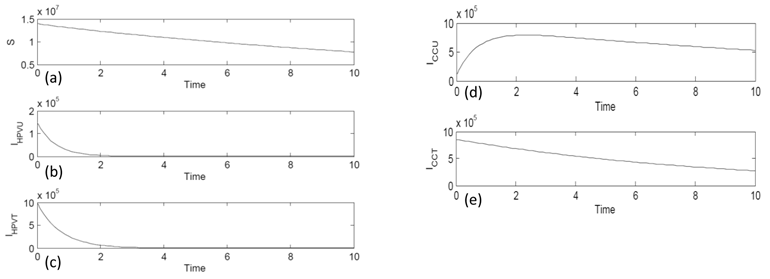
All state equations in the model were approximated using the Runge-Kutta 4th order numerical approximation method using MatLab software. Figure 2 (a) shows the behavior of the susceptible compartment (S) with time. The graph is decreasing and has a negative slope. As time increases the number of those susceptible decreases but never disappears. Figure 2 (b) is the compartment of HPV infected without treatment (IHPVU). With time it gets very close to zero to almost nonexistent. This is because the body could have naturally healed. Figure 2 (c) is of the compartment of HPV infected with treatment (IHPVT). The graph decreases over time because there are more treatment options such as vaccines and surgery. Figure 2 (d) is of the compartment of cervical cancer untreated (ICCU). The graph increases then decreases and gets closer but never reaches zero. Figure 2 (e) is of the compartment of cervical cancer with treatment (ICCT). The graph steadily decreases with time because the survival rate with treatment is high.
Simulation Graph Results of the five compartments: (a) the Susceptible (S) population compartment, (b) HPV infected untreated (IHPVU) compartment, (c) HPV infected with treatment (IHPVT) compartment, (d) Cervical Cancer untreated (ICCU) compartment, and (e) Cervical Cancer with treatment (ICCT) compartment.
The basic reproductive number R0U is a directly proportional rate of infectivity of HPV HPVU and the contact rate in which a human infects another human with HPV and indirectly proportional to the recovery rate plus the mortality by natural causes and the disease. R0T is directly proportional to the rate of infectivity of HPVT and contact rate in which an infected person infects another person with HPV and indirectly proportional to the recovery rate plus the mortality from HPV related causes and natural causes. This model shows that there is a direct relationship between HPV and cervical cancer. These results can be used to test the efficacy of new methods of treatment that will decrease the rate of infectivity of HPV and cervical cancer with time.
Mathematical models, from individual and population perspectives, will help decision makers to evaluate different prevention and mitigation scenarios of HPV. It can deploy synergistically to improve cancer outcomes, reduce disparities, and enhance the cost-effectiveness of CC control. Integrating the best-available epidemiologic data, computer-based mathematical models used in a decision-analytic framework can identify those factors most likely to influence outcomes and can inform decisions that need to be made amidst considerable lack of data and uncertainty.
Given the inevitable uncertainty around input parameters to any mathematical model, an important feature of many modeling efforts is the calibration of these parameter values in reference to observed epidemiologic data.
Competing Interests
The authors have declared that no competing interest exists.
References
1. Genital HPV infection: CDC fact sheet. Centers for Disease Control and Prevention. http://www.cdc.gov/std/HPV/STDFact-HPV.htm
2. Walboomers JM, Jacobs MV, Manos MM, Bosch FX, Kummer JA, Shah KV, Snijders PJ, Peto J, Meijer CJ, Munoz N. Human papillomavirus is a necessary cause of invasive cervical cancer worldwide. J Pathol. 1999;189(1):12-19
3. zur Hausen H. Papillomaviruses causing cancer: Evasion from host-cell control in early events in carcinogenesis. J Natl Cancer Inst. 2000;92:690-698
4. Clifford GM, Smith JS, Plummer M, Munoz N, Franceschi S. Human papillomavirus types in invasive cervical cancer worldwide: A meta-analysis. Br J Cancer. 2003;88:63-73
5. Ho GY, Bierman R, Beardsley L, Chang CJ, Burk RD. Natural history of cervicovaginal papillomavirus infection in young women. N Engl J Med. 1998;338:423-428
6. Human Papilloma Virus (HPV), Cancer, and HPV Vaccines-Frequently Asked Questions; Medical Review: 01/07/2009. American Cancer Society. http://www.cancer.org/docroot/CRI/content/CRI_2_6x_FAQ_HPV_Vaccines.asp
7. Atkinson W, Wolfe S, Hamborsky J. Epidemiology and Prevention of Vaccine-Preventable Diseases; 12th ed, second printing. Washington DC: Public Health Foundation. 2012
8. Diekmann O, Heesterbeek JAP, Metz JAJ. On the definition and the computationof the basic reproduction ratio R0, in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990;28:365- 382
9. US Census Bureau. American Community Survey. US: US Census Bureau. 2010
Author contact
![]() Corresponding author: Ana M. Tameru, Ph. D., Department of Mathematics and Computer Science, Alabama State University, 915 S. Jackson St., Montgomery, AL 36101. tel: (334) 229-6828. e-mail: atameruedu.
Corresponding author: Ana M. Tameru, Ph. D., Department of Mathematics and Computer Science, Alabama State University, 915 S. Jackson St., Montgomery, AL 36101. tel: (334) 229-6828. e-mail: atameruedu.

 Global reach, higher impact
Global reach, higher impact